Polynomial Interpolation Using FFT

Use the fast Fourier transform (FFT) to estimate the coefficients of a trigonometric polynomial that interpolates a set of data.

FFT in Mathematics

The FFT algorithm is associated with applications in signal processing, but it can also be used more generally as a fast computational tool in mathematics. For example, coefficients c_i of an nth degree polynomial $c_{1} x^{n} + c_{2} x^{n - 1} + ... + c_{n} x + c_{n + 1}$ that interpolates a set of data are commonly computed by solving a straightforward system of linear equations. While studying asteroid orbits in the early 19th century, Carl Friedrich Gauss discovered a mathematical shortcut for computing the coefficients of a polynomial interpolant by splitting the problem up into smaller subproblems and combining the results. His method was equivalent to estimating the discrete Fourier transform of his data.

Interpolate Asteroid Data

Open Live Script

In a paper by Gauss, he describes an approach to estimating the orbit of the Pallas asteroid. He starts with the following twelve 2-D positional data points x and y.

x = 0:30:330;
y = [408 89 -66 10 338 807 1238 1511 1583 1462 1183 804];
plot(x,y,'ro')
xlim([0 360])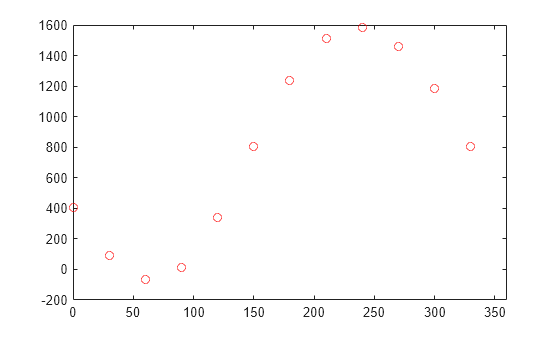

Figure contains an axes object. The axes contains a line object which displays its values using only markers.

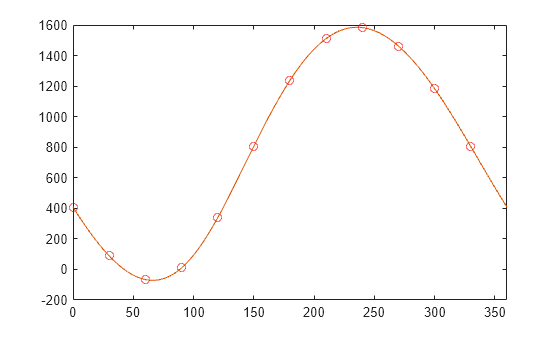
Gauss models the asteroid's orbit with a trigonometric polynomial of the following form.

$\begin{array}{rcl} y = a_{0} & + & a_{1} \cos (2 π (x / 360)) + b_{1} \sin (2 π (x / 360)) \\ a_{2} \cos (2 π (2 x / 360)) + b_{2} \sin (2 π (2 x / 360)) \\ \dots \\ a_{5} \cos (2 π (5 x / 360)) + b_{5} \sin (2 π (5 x / 360)) \\ a_{6} \cos (2 π (6 x / 360)) \end{array}$

Use fft to compute the coefficients of the polynomial.

m = length(y);
n = floor((m+1)/2);
z = fft(y)/m;

a0 = z(1); 
an = 2*real(z(2:n));
a6 = z(n+1);
bn = -2*imag(z(2:n));

Plot the interpolating polynomial over the original data points.

hold on
px = 0:0.01:360;
k = 1:length(an);
py = a0 + an*cos(2*pi*k'*px/360) ...
        + bn*sin(2*pi*k'*px/360) ...
        + a6*cos(2*pi*6*px/360); 

plot(px,py)

Figure contains an axes object. The axes object contains 2 objects of type line. One or more of the lines displays its values using only markers

References

[1] Briggs, W. and V.E. Henson. The DFT: An Owner's Manual for the Discrete Fourier Transform. Philadelphia: SIAM, 1995.

[2] Gauss, C. F. “Theoria interpolationis methodo nova tractata.” Carl Friedrich Gauss Werke. Band 3. Göttingen: Königlichen Gesellschaft der Wissenschaften, 1866.

[3] Heideman M., D. Johnson, and C. Burrus. “Gauss and the History of the Fast Fourier Transform.” Arch. Hist. Exact Sciences. Vol. 34. 1985, pp. 265–277.

[4] Goldstine, H. H. A History of Numerical Analysis from the 16th through the 19th Century. Berlin: Springer-Verlag, 1977.